Généralités sur la fonction exponentielle

Définition

Théorème

Il existe une unique fonction $f$ définie et dérivable sur $\R$ vérifiant, pour tout nombre réel $x$,:

$\boxed{f'(x)=f(x)}$ et $\boxed{f(0)=1}$.

Cette fonction $f$ vérifiant $f'=f$ et $f(0)=1$ est appelée fonction exponentielle.

La fonction exponentielle est la fonction, notée $exp$, définie et dérivable sur $\R$ telle que:

$\boxed{exp(0)=1}$ et $\boxed{exp'=exp}$

Propriétés algébriques

Théorème

Pour tous nombres réels $x$ et $y$, $\boxed{exp(x+y)=exp(x) \times exp(y)}$.

Cette relation s'appelle relation fonctionnelle.

Autrement dit: l'exponentielle d'une somme de deux nombres est le produit de l'exponentielle de chacun de ces nombres .

Remarque

Cette formule permet de transformer les sommes en produits et réciproquement.

Propriété

Pour tous réels $x$ et $y$, on a :

• $exp(-x) \times exp(x)=1 \iff \boxed{exp(-x)=\frac{1}{exp(x)}}$

• $\boxed{exp(x-y)=\frac{exp(x)}{exp(y)}}$

• $\boxed{(exp(x))^n=exp(nx)}$

Exemples:

$\left(\exp(1)-\exp(-1)\right)^2=(\exp(1))^2-2\exp(1)\exp(-1)+(\exp(-1))^2$
$=\!\exp(1\!\times\!2)\!-\!2\exp(1\!-\!1)\!+\!\exp(-1\!\times\!2)\!=\!\exp(2)\!-\!2\exp(0)\!+\!\exp(-2)\!=\!\exp(2)\!-\!2\!+\!\exp(-2)$.

Notation puissance

Toutes ces propriétés rappellent celles des puissances, en effet, on rappelle que :

• $a^n \times a^m = a^{n+m}$

• $(a^n)^m=a^{nm}$

• $\frac{a^n}{a^m}=a^{n-m}$

• $a^0=1$ et $a^1=a$

Les propriétés de la fonction $exp$ étant ressemblantes, on décide de noter la fonction exponentielle de façon plus simple :

$exp(x)=e^x$ pour tout $x$

On écrit alors les propriétés algébriques précédentes de la façon suivante :

• $e^0=1$ et $e^1=e$

• $e^{x+y}=e^x \times e^y$

• $(e^x)^n=e^{nx}$, avec $n \in \N$

• $\frac{e^x}{e^y}=e^{x-y}$

Remarque : Le nombre $e$

Le nombre $e^1$ est noté $e$. Une valeur approchée de ce nombre au millième est $2,718$.

Exercice d'application 1

Simplifier les écritures suivantes

1. $A=\frac{e^{3x} \times (e^x)^5}{e^{x-2}}$

2. $B=\frac{e \times e^{2x-1}}{2e^{-x+2}}$

Exercice d'application 2

Démontrer que pour tout $x \in \R$, on : $\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}$

Lien avec les suites géométriques

De la propriété : $(e^x)^n=e^{nx}$, avec $n \in \N$, on en déduit que :

Soit $a$ un réel et $(u_n)$ la suite de terme général $e^{na}$ où $n$ est un entier naturel.

La suite $(u_n)$ est une suite géométrique de premier terme $u_0=1$ et de raison $e^a$.

Exercice d'application

Soit $(u_n)$ la suite définie par $u_n=10 \times e^{3n}$ pour tout $n \in \N$.

1. Calculer $u_0$

2. Montrer que $(u_n)$ est une suite géométrique dont on donnera le premier terme et la raison.

3. Justifier que la suite est croissante puis déterminer à partir de quel rang on a : $u_n>10^6$

On peut aussi écrire un algorithme de seuil

A connaitre

    #Algorithme de seuil
    from math import *

    #initialisation
    n = 0
    u = 10
    #boucle pour calculer les termes de la suite jusqu'à ce que le seuil soit franchi
    while u<10**6:
        n = n+1
        u = 10*exp(3*n)
    print(n)

Étude de la fonction exponentielle

La fonction exponentielle

Propriété

Pour tout nombre réel $x$, $\boxed{e^x>0}$

Propriété

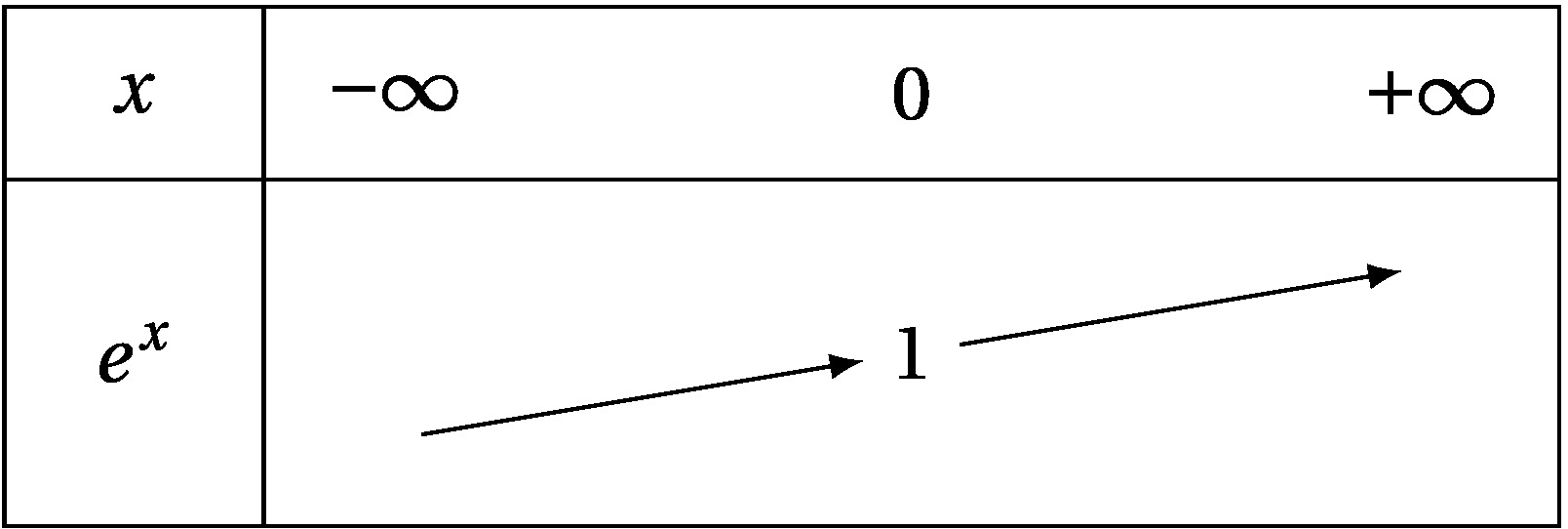
La fonction exponentielle est dérivable sur $\R$ et $\boxed{(e^x)'=e^x}$.

La fonction exponentielle est strictement croissante sur $\R$

Illustration graphique et tableau de variations

Remarques:

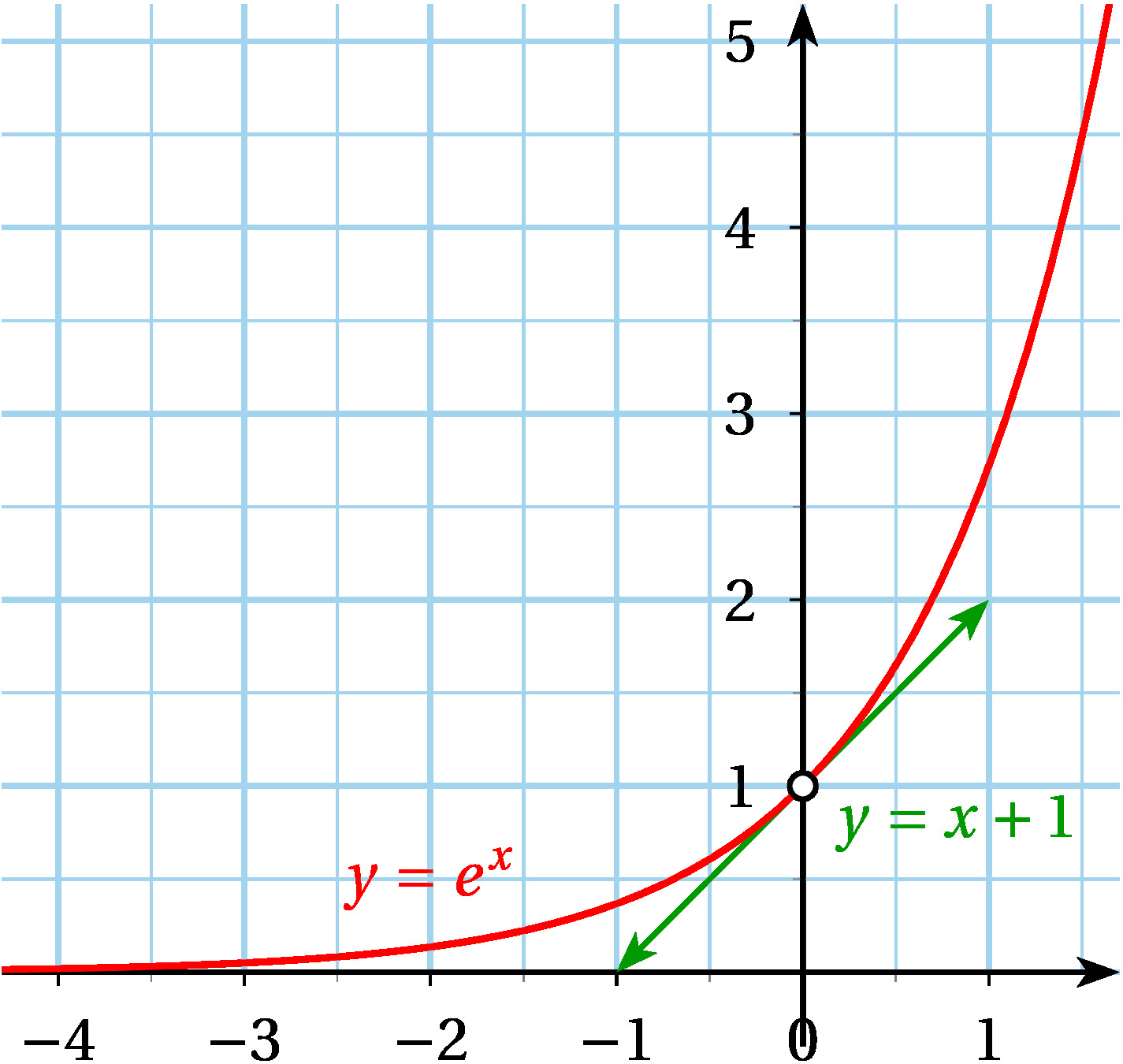
La droite d'équation $y=x+1$ est tangente à la courbe représentative au point d'abscisse 0.

En effet l'équation de la tangente à la courbe au point $0$ est :

$y=f'(0)(x-0)+f(0) \iff y=e^0 \times x+e^0=1 \times x + 1\iff y=x+1$

Résolution d'équations et d'inéquations

De la stricte croissance de la fonction exponentielle, on déduit que :

Propriété

Pour tous réels $a$ et $b$, on a:

• $\boxed{e^a = e^b \iff a=b}$

• $\boxed{e^a \leq e^b \iff a \leq b}$

METHODE : savoir résoudre des équations et des inéquations avec des exponentielles

Pour résoudre une équation d'inconnue $x$ réel comportant des exponentielles :

On essaye selon le cas de se ramener à :

Une équation de la forme $e^{u(x)} = e^{v(x)}$ où $u$ et $v$ sont deux fonctions.

Alors, $e^{u(x)} = e^{v(x)} \Leftrightarrow u(x)=v(x)$ et, éventuellement, $u(x)=v(x) \Leftrightarrow u(x)-v(x)=0$.

La méthode est analogue pour résoudre une inéquation.

Exercice d'application:

Déterminer l'ensemble $\mathcal{S}$ des solutions des équations et inéquations.

1. $e^{x^2+2x-3} = 1$
2. $2e^{2x}-e^x-1=0$
3. $e^{\sqrt{3x-5}} <e$
4. $\dfrac{e^{2x+1}}{^{x-4}}\geqslant e^{x^2-1}$

Fonctions définies par $f(x)=e^{-kx}$ et $f(x)=e^{kx}$

De façon générale, les fonctions définies par $f(x)=e^{-ax+b}$ et $f(x)=e^{ax+b}$, où $a$ et $b$ sont des entiers relatifs, sont appelées fonctions exponentielles.

Propriété

Pour tous réels $a$ et $b$ fixés,

• la fonction $f$ définie sur $\R$ par $f(x)=e^{ax+b}$ est dérivable sur $\R$ et, pour tout réel $x$, $f'(x)=ae^{ax+b}$.

• la fonction $f$ définie sur $\R$ par $f(x)=e^{-ax+b}$ est dérivable sur $\R$ et, pour tout réel $x$, $f'(x)=-ae^{-ax+b}$.

Exemple:

La fonction $h$ définie sur $\R$ par $h(x)=-3e^{2x-5}+1$ est dérivable sur $\R$ et, pour tout réel $x$, $h'(x)=2 \times (-3e^{2x-5})=-6e^{2x-5}$.

Pour tout réel $x$ , $e^{2x-5}>0$, donc on en déduit que $h'(x)<0$.

Par conséquent, $h$ est strictement décroissante sur $\R$.

Exercice d'application :

Étudier les variations des fonctions $f$ et $g$ définies sur $\R$ par :

• $f(x)=e^{x+1}+x$

• $g(x)=e^{-2x+6}$