24-NSIJ1ME1-Ex3 correction

Partie A

1. Code:

chien40 = Chien(40, "Duke", "weel dog", 10)

2. Code:

def changer_role(self, nouveau_role):
    """Change le rôle du chien avec la valeur passée en paramètre."""
    self.role = nouveau_role

3. Code:

chien40.changer_role("leader")

Partie B

4. Code:

def retirer_chien(self, numero):
    nouvelle_liste_chien = []
    for chien in self.liste_chien:
        if chien.id_chien != numero:
            nouvelle_liste_chien.append(chien)
    self.liste_chien = nouvelle_liste_chien

Autre version, en utilisant les listes par compréhension:

def retirer_chien(self, numero):
    self.liste_chien = [chien in self.liste_chien if chien.id_chien != numero]

5. Code:

eq11.retirer_chien(46)

6. D'après le code fournit, convert('4h36') donne $4 + (3 + 6)/60= 4 + 9/60 = 4.15$

7. Code:

def temps_course(equipe):
    temps_total = 0
    for temps in equipe.liste_temps:
        temps_total += convert(temps)
    return temps_total

Partie C

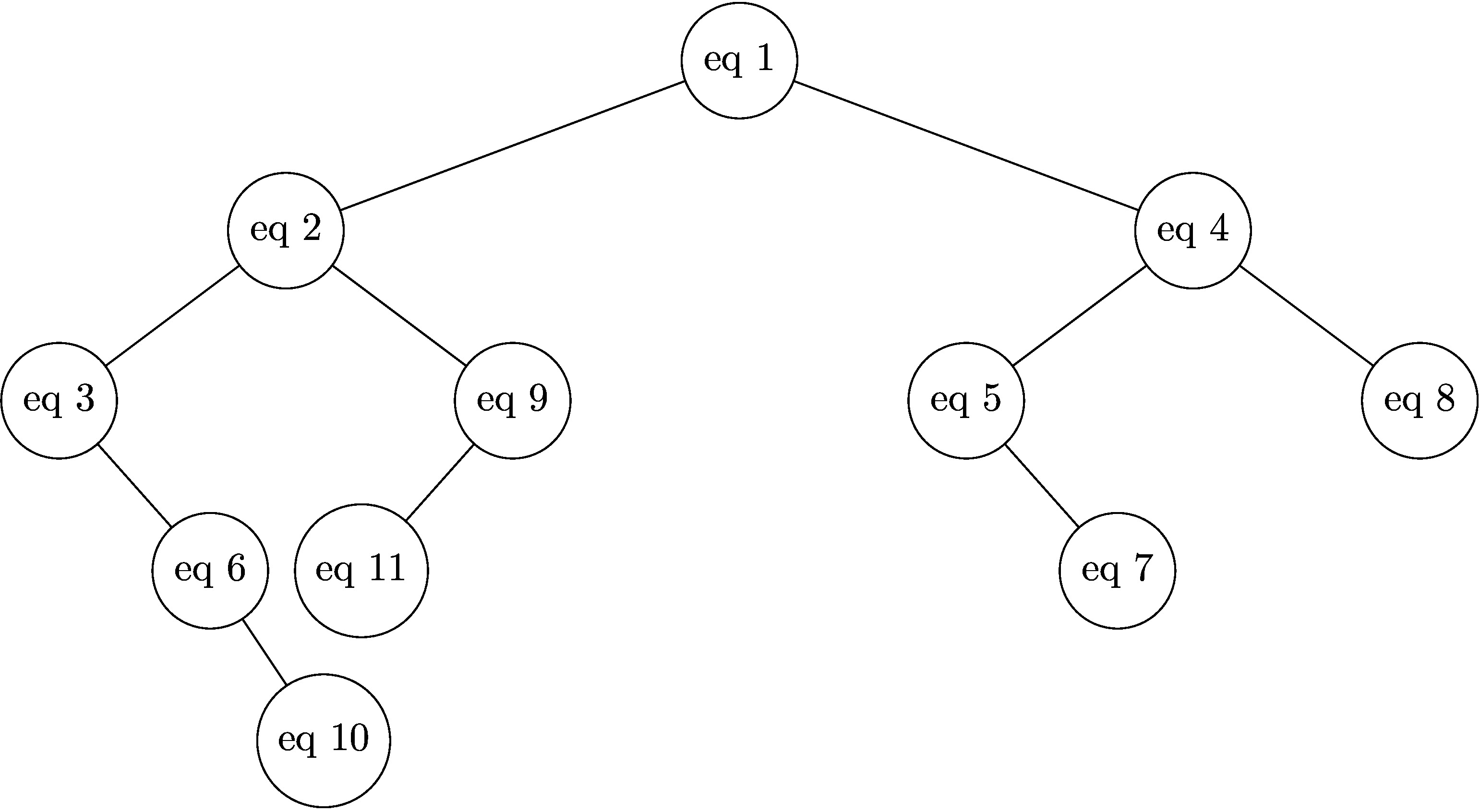
8. Le plus simple ici est de trier les équipes par temps croissant pour faciliter la création de l'arbre.

• eq1: 7
• eq2: 4
• eq3: 1
• eq4: 10
• eq5: 8
• eq6: 2
• eq7: 9
• eq8: 11
• eq9: 6
• eq10: 3
• eq11: 5

9. Le parcours infixe permet d'obtenir les valeurs d'un ABR par ordre croissant.

10. La fonction insererest récursive car elle s'appelle elle-même.

11. Code:

def inserer(arb, eq):
    """ Insertion d'une équipe à sa place dans un ABR contenant
    au moins un noeud."""
    if convert(eq.temps_etape) < convert(arb.racine.temps_etape):
       if arb.gauche is None:
           arb.gauche = Noeud(eq)
       else:
           inserer(arb.gauche, eq)
    else:
       if arb.droit is None:
            arb.droit = Noeud(eq)
       else:
            inserer(arb.droit, eq)

12. Code:

def est_gagnante(arbre):
     if arbre.gauche == None:
       return arbre.racine.nom_equipe
     else:
       return est_gagnante(arbre.gauche)

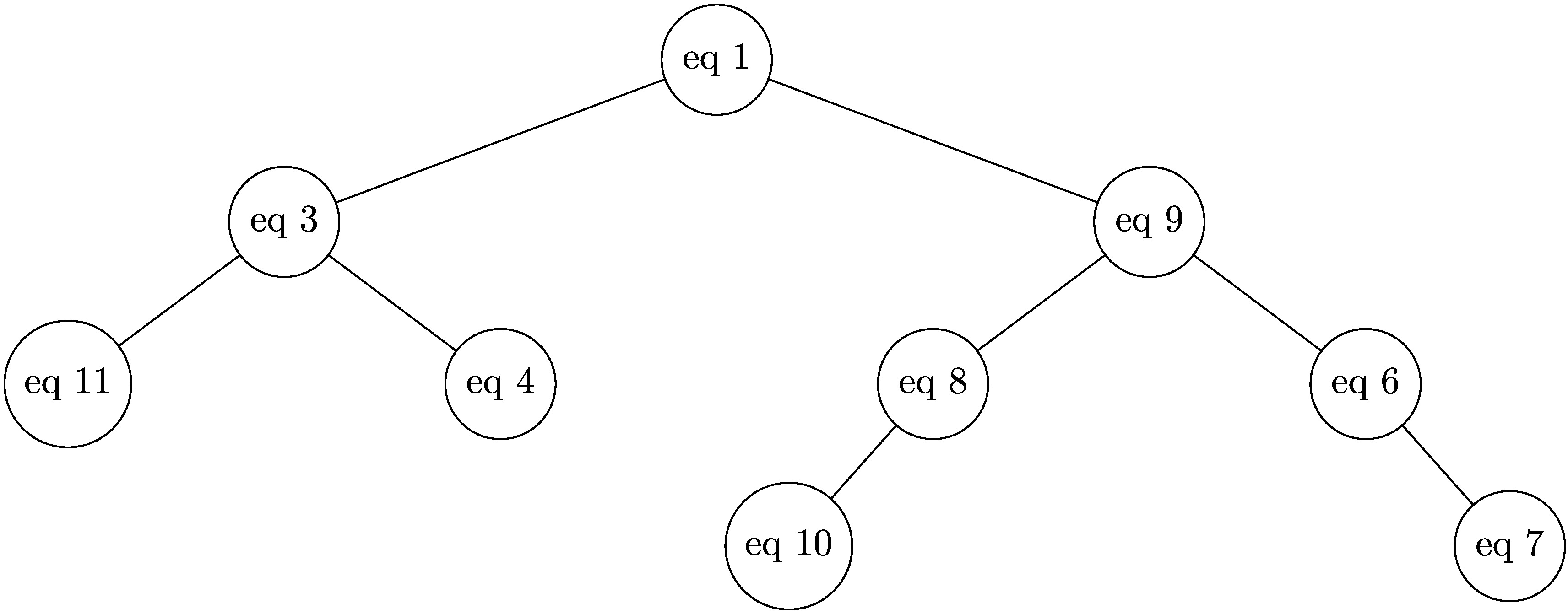
13. eq2 n'a qu'un fils droit. Donc on supprime eq2 et on relie son successeur eq3 à eq1.

eq5 a deux fils, on le remplace par son successeur, c'est-à-dire l'équipe qui a le temps immédiatement supérieur, qui est le minimum de ses descendants droits.

Ici c'est eq9 qui est le minimum des descendants droits.

14. Code:

def rechercher(arbre, equipe):
    if arbre is None:
        return False
    if arbre.racine == equipe:
        return True
    if convert(equipe.temps_etape) < convert(arbre.racine.temps_etape):
        return rechercher(arbre.gauche, equipe)
    else:
        return rechercher(arbre.droit, equipe)